Globálne sa stretávame s narastajúcimi problémami so stabilitou elektrizačných sústav v dôsledku prechodu na nízkouhlíkové energetické sústavy. Tie sú charakterizované vysokým podielom zdrojov využívajúcich výkonovú elektroniku, označovaných ako CIG (converter-interfaced generation) alebo IGB (inverter-based generation), prepojených s obnoviteľnými zdrojmi energie (OZE), distribuovanými energetickými zdrojmi (DEZ), úložiskami a flexibilnými záťažami, akou je napríklad elektromobilita. Tieto sústavy zahŕňajú aj inteligentné sieťové technológie, ako sú inteligentné merače, automatizované rozvodne, mikrosiete a IoT a v neposlednom rade distribuované obchodné platformy, virtuálne elektrárne a pod. Ide o obojsmerný prenos energie a dát v rámci konceptu prosumer. Prepojená povaha týchto technológií vedie k zložitým interakciám medzi tradičnými a novými technológiami, čo ovplyvňuje rozhodovanie o investíciách a prevádzkových postupoch. Skúsenosti z krajín s vysokým podielom obnoviteľných zdrojov, ako sú Austrália, Veľká Británia a Írsko, ukazujú systémovú závislosť medzi tradičnými a novými technológiami, čo vytvára zložité dynamické interakcie vyžadujúce nové prístupy k riadeniu, kontrole a prevádzke na udržanie stability elektrizačnej sústavy a tým aj jej bezpečnosti a spoľahlivosti. Tieto faktory významne ovplyvňujú dynamiku sústavy, najmä pokiaľ ide o okamžitý mix výroby, čo má vplyv na systémovú zotrvačnosť (uložená energia v synchrónne rotujúcich zariadeniach), skratovú odolnosť a rezervu jalového výkonu.
Pri diskusiách o stabilite sústavy sa dostal do popredia relatívne nový pojem flexibilita sústavy. Pri dosahovaní flexibility sústavy potrebnej na prispôsobenie variabilnej a distribuovanej výroby elektriny z OZE má zásadnú úlohu spotrebiteľ. Flexibilita je považovaná za schopnosť riadenia zdrojov v elektrizačnej sústave, ktoré slúžia na zmiernenie zmien a neistôt v systéme [1].
Reklasifikácia stability
V auguste 2004 zverejnil inštitút IEEE rozsiahlu štúdiu, ktorá sa podrobne venovala definíciám a klasifikácii stability elektrických systémov. Táto štúdia bola výsledkom spolupráce medzi IEEE a výborom CIGRE, pričom na nej pracovala spoločná pracovná skupina, ktorá zohľadnila vtedajšie technologické a prevádzkové podmienky elektrizačných sústav [2].
Technologický pokrok, rýchly rozvoj obnoviteľných zdrojov energie a ich integrácia do distribučných a prenosových sústav priniesli nové výzvy a potrebu aktualizácie pôvodnej štúdie. Po takmer dvoch desaťročiach bolo zrejmé, že je nevyhnutné celú štúdiu prepracovať, aby lepšie odrážala súčasné podmienky a výzvy. Preto pracovná skupina IEEE PES-TR77 (Power System Dynamic Performance Committee) zverejnila v máji 2020 novú správu s názvom Definície stability a charakteristika dynamiky správania v systémoch s vysokým prienikom výkonovej elektroniky [3].
Táto správa predstavuje zásadný posun v chápaní stability elektrizačných sústav, pretože zohľadňuje nielen tradičné synchrónne stroje, ale aj nové technológie, ktoré dominujú v moderných sústavách. Systémy s vysokým prienikom výkonovej elektroniky, ako sú solárne a veterné elektrárne s výkonovou elektronikou, vyžadujú nové prístupy k hodnoteniu stability, pretože ich dynamické správanie sa zásadne líši od tradičných zdrojov energie. Nová správa IEEE PES-TR77 preto poskytuje aktualizované definície a metodiky, ktoré sú nevyhnutné pre moderné elektrizačné sústavy, a zároveň poukazuje na potrebu ďalšieho výskumu a vývoja v tejto oblasti, aby sa zabezpečila spoľahlivosť a bezpečnosť budúcich energetických systémov.
Štúdia [3] sa zameriava na dve časové škály, a to na elektromagnetické a elektromechanické prechodné javy, a jej súčasťou je reklasifikácia a doplnenie jednotlivých typov stability v kontexte dosahu OZE s CIG (obr. 1).
Obr. 1 znázorňuje časové škály pre rôzne triedy dynamických javov v elektrizačných sústavách. Časový rozsah týkajúci sa riadenia zariadení s CIG sa pohybuje od niekoľkých mikrosekúnd až po niekoľko milisekúnd, teda zahŕňa vlnové a elektromagnetické javy. Ak vezmeme do úvahy penetráciu CIG, tak rýchlejšia dynamika získa na dôležitosti pri analýze budúceho dynamického správania energetického systému v porovnaní s javmi v časovom rozmedzí niekoľkých milisekúnd až minút. Zameranie sa na časový rozsah elektromechanických prechodových javov umožnilo niekoľko zjednodušení v systéme modelovania zdrojov, čo výrazne pomohlo pri analýze súvisiacich javov.
Klasifikácia stability elektrizačnej sústavy je založená na vnútornej dynamike javov vedúcich k problémom so stabilitou. Klasifikácia do časových stupníc sa vzťahuje na komponenty, javy a riadenia, ktoré je potrebné modelovať, aby sa správne reprodukoval analyzovaný problém. Vplyvmi distribuovaných zdrojov pripojených na distribučnej úrovni na prenosovú sústavu sa zaoberá štúdia [5], a preto sú analyzované osobitne. Okrem toho sa správa [3] nezaoberá 1) prípadmi, keď nesprávne nastavenie riadenia spôsobuje miestnu nestabilitu, 2) prípadmi, keď nestabilitu riadiacej slučky možno priamo charakterizovať bez modelovania energetického systému, 3) otázkami stability spojenými s mikrosieťami (táto téma je riešená napr. v [6]), 4) javmi šírenia elektromechanických a elektromagnetických vĺn [7], [8].
Pôvodná štúdia o stabilite [2] klasifikovala stabilitu elektrizačných sústav do troch rôznych foriem stability: uhlová stabilita rotora, stabilita napätia a stabilita frekvencie. Každá forma stability je rozdelená na stabilitu malých a stabilitu veľkých porúch. Je stanovený aj vzťah medzi krátkodobou stabilitou, dlhodobou stabilitou a vyššie uvedenými formami stability. Aktualizovaná štúdia [3] rozšírila triedy stability o dve nové kategórie: elektrická rezonančná stabilita a stabilita riadená meničom (obr. 2).
Kľúčovým aspektom týchto zjednodušení je predpoklad, že napätiu a prúdu dominuje základná frekvenčná zložka systém (50, resp. 60 Hz). Preto možno elektrizačnú sústavu modelovať s ohľadom na fázory napätia a prúdu v ustálenom stave, čo poznáme pod pojmom kvázistacionárny prístup modelovania (obr. 3). S týmto prístupom modelovania sú vysokofrekvenčná dynamika a dynamika spojená so spínaním výkonovej elektroniky reprezentované buď modelmi v ustálenom stave, alebo zjednodušenými dynamickými modelmi. Z toho vyplýva, že rýchle javy, ako napríklad prepínanie, nemožno úplne zachytiť. Vzhľadom na uvedené časové rozsahy prevádzky súvisiace s CIG existuje potreba rozšíriť šírku pásma skúmaných javov a zahrnúť rýchlejšiu dynamiku v rámci elektromagnetických časových škál (obr. 1).
Formálna definícia stability elektrizačnej sústavy je teda nasledujúca: „Stabilita energetického systému je schopnosť elektrického energetického systému pri danom začiatočnom prevádzkovom stave znovu získať stav prevádzkovej rovnováhy po vystavení fyzickému narušeniu, pričom väčšina systémových premenných je ohraničená tak, že prakticky celý systém zostáva neporušený.“ [3].
Stabilita uhla rotora
Stabilita uhla rotora sa týka schopnosti vzájomne prepojených synchrónnych strojov v napájacom systéme zostať v synchronizácii za normálnych prevádzkových podmienok (počas ktorých sú vystavené malému alebo veľkému rušeniu) a znovu získať synchronizáciu [3]. Stroj udržiava synchronizmus, ak je elektromagnetický krútiaci moment rovný a opačný ako mechanický krútiaci moment dodávaný hnacím motorom. Preto tento typ stability závisí od schopnosti synchrónnych strojov udržiavať alebo obnovovať rovnováhu medzi týmito dvoma protichodnými krútiacimi momentmi.
Synchrónne stroje udržiavajú stabilitu obnovením síl v okamihu, keď porucha spôsobí, že jeden alebo viac strojov zrýchli alebo spomalí svoju činnosť v porovnaní s ostatnými. V ustálených podmienkach existuje rovnováha medzi vstupným mechanickým krútiacim momentom a vyvažovacím elektromagnetickým krútiacim momentom každého stroja a otáčkami všetkých prepojených strojov. Porucha naruší túto rovnováhu a vedie k nevyváženosti krútiaceho momentu, čo má za následok zrýchlenie alebo spomalenie rotorov synchrónnych strojov podľa zákona pohybu rotujúceho telesa. V dôsledku toho sa uhol rotora synchrónneho stroja (strojov) môže zvýšiť nad maximálnu hodnotu a stroj (stroje) tzv. vypadne zo synchronizmu (out of step) vzhľadom na ostatné stroje. Výrazné zvýšenie rýchlosti strojov však nemusí nevyhnutne viesť k strate synchronizmu, ak všetky stroje zrýchľujú alebo spomaľujú spolu. Kľúčovým faktorom pri určovaní stability systému je rozdiel uhla medzi strojom alebo skupinou strojov a zvyškom systému [9].
Stabilita uhla rotora s malým rušením je schopnosť energetického systému udržiavať synchronizmus pri malých poruchách, ako sú malé zmeny zaťaženia a výroby. Malé poruchy sú tie zmeny, pri ktorých sú odchýlky uhlov rotorov synchrónnych strojov od rovnovážneho bodu také malé, že systémové rovnice môžu byť lineárne okolo rovnovážneho bodu bez toho, aby viedli k významným chybám. Časový rámec, v ktorom sa očakáva, že sa oscilácie uhla rotora po malom narušení zoslabia, je menší ako 20 sekúnd [10], [11].
Prechodná stabilita uhla rotora je schopnosť energetického systému udržiavať synchronizmus pri vystavení závažným poruchám, ako je skrat na prenosovom vedení či odpojenie veľkých elektrární alebo veľkých záťaží. Reakcia systému zahŕňa veľké odchýlky uhlov rotorov synchrónnych strojov. V dôsledku toho už nie je vhodné linearizovať systémové rovnice ako v prípade malých porúch, pričom vývoj uhlov rotorov sa zvyčajne analyzuje pomocou metód numerickej integrácie. Stabilita v tomto prípade závisí od začiatočného prevádzkového stavu systému a od závažnosti poruchy. Ustálený stav po poruche sa zvyčajne líši od prevádzkového bodu pred poruchou. Časový rámec v štúdiách prechodnej stability je zvyčajne kratší ako 10 sekúnd po poruche, aj keď v prípade rozsiahlych prepojených sústav môže byť tento časový rámec predĺžený na 20 sekúnd [3].
Napäťová stabilita
Napäťová stabilita sa vzťahuje na schopnosť elektrizačnej sústavy udržiavať stabilné napätie na všetkých zberniciach (uzloch) v systéme po poruche. Závisí to od schopnosti kombinovaných výrobných a prenosových sústav poskytovať energiu požadovanú záťažou. Táto schopnosť je obmedzená maximálnym prenosom energie do konkrétnej skupiny uzlov a je spojená s poklesom napätia, ku ktorému dochádza, keď činný a/alebo jalový výkon prúdi cez induktívne reaktancie prenosovej sústavy.
Krátkodobá stabilita napätia zahŕňa dynamiku rýchlo pôsobiacich komponentov sústavy, ako sú indukčné motory, elektronicky riadené záťaže, ZVN jednosmerné prenosové vedenia a CIG generátory. Časové pásmo rádovo niekoľko sekúnd je podobné stabilite uhla rotora alebo stabilite poháňanej meničom (typ pomalej interakcie). Preto treba použiť modely s príslušným stupňom detailu. Pre krátkodobú stabilitu napätia je nevyhnutné dynamické modelovanie zaťaženia a hlavným problémom sú skraty v blízkosti záťaže. Najbežnejším prípadom krátkodobej napäťovej nestability je zastavenie indukčných motorov po veľkej poruche buď stratou rovnováhy (medzi elektromagnetickými a mechanickými krútiacimi momentmi), alebo nedostatočnou „príťažlivosťou“ k rovnovážnemu bodu v dôsledku neskorého vypnutia poruchy [3].
Dlhodobá stabilita napätia zahŕňa vplyv pomalšie pôsobiacich javov, ako sú prepínanie odbočiek transformátorov, termostaticky regulované záťaže a obmedzovače prúdu generátorov. Časový úsek prechodného javu sa môže predĺžiť na niekoľko minút a na analýzu dynamického výkonu systému sú potrebné dlhodobé simulácie. Tento typ stability zvyčajne nie je spôsobený počiatočnou poruchou, ale výpadkom prenosového a/alebo výrobného zariadenia po odstránení poruchy a následnou stratou dlhodobej rovnováhy. Dlhodobá nestabilita nastáva, keď sa dynamika zaťaženia pokúsi obnoviť spotrebu energie nad maximálnu hranicu prenosu. Nestabilita môže nastať aj vtedy, keď nápravné opatrenie nie je schopné včas obnoviť stabilnú rovnováhu po narušení, a preto nie je návrat k rovnováhe možný. Alternatívne by narušenie rovnováhy vedúce k nestabilite mohlo byť spôsobené aj trvalým zvyšovaním zaťaženia (napr. zvýšenie ranného zaťaženia) [9], [10], [11].
Frekvenčná stabilita
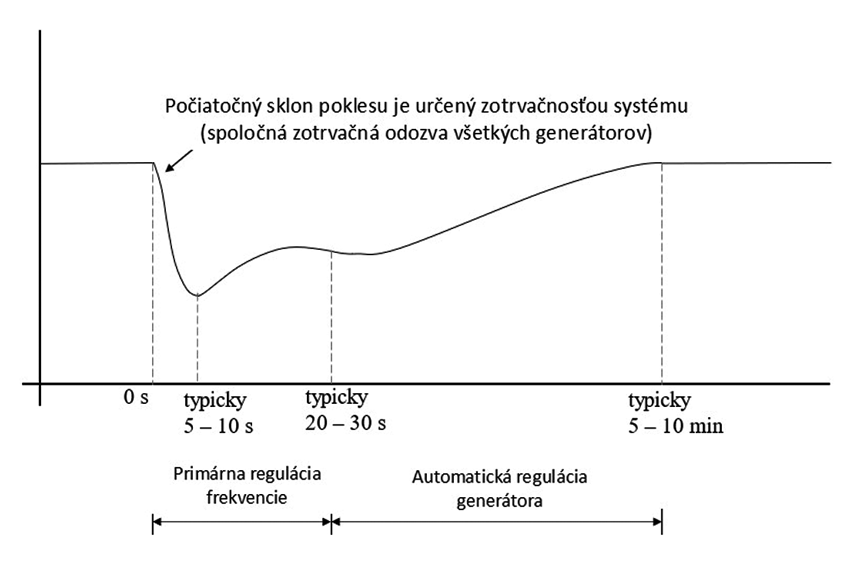
V prepojenej elektrizačnej sústave, v ktorej dominuje synchrónna výroba, má prvoradý význam regulácia frekvencie. Najčastejšie analyzované udalosti sú tie, ktoré spôsobujú pokles systémovej frekvencie. Obr. 4 znázorňuje tri odlišné periódy počas udalosti, ktorá spôsobuje pokles frekvencie a s tým súvisiace ovládacie prvky: 1) začiatočnú zotrvačnú reakciu synchrónnych generátorov, 2) primárnu frekvenčnú reakciu generátorov a tlmenie zaťaženia a 3) automatické riadenie generátorov, ktoré vráti frekvenciu späť na jej nominálnu hodnotu.
Zotrvačná reakcia systému je prirodzenou fyzickou reakciou synchrónnej výroby na náhlu nerovnováhu medzi výrobou a spotrebou. Ak dôjde napríklad k náhlemu nútenému výpadku veľkého generátora v okamihu, ktorý nasleduje po strate výroby, zaťaženie sa okamžite nezmení. Výsledkom je, že v dôsledku základných fyzikálnych princípov (a nie ovládacích prvkov) budú všetky zostávajúce synchrónne generátory reagovať v pomere k ich elektrickej blízkosti, zotrvačnosti a elektrickému výkonu, aby poskytli časť celkového strateného výkonu na pokračovanie v napájaní záťaže. Po tejto extrémne rýchlej elektrickej reakcii spôsobí dodatočná elektrická energia dodávaná každým synchrónnym generátorom z uloženej rotačnej kinetickej energie v rotoroch generátorov nerovnováhu medzi elektrickým a mechanickým krútiacim momentom na hriadeli každého generátora, čím sa spomalia všetky generátory, čo vedie k začiatočnému rozpadu frekvencie systému. Ide o inherentnú zotrvačnú reakciu synchrónnych generátorov v dôsledku fyzikálnych zákonov a nie zásahov riadenia. Táto nekontrolovaná frekvenčná reakcia je prvou fázou reakcie znázornenej na obr. 4.
Za predpokladu, že by boli všetky generátory bez riadenia, systémová frekvencia by naďalej klesala, aktivovali by sa schémy odopínania záťaže a ostatné ochranné prvky, čo by v extrémnom prípade viedlo k výpadku systému. Aby sa predišlo týmto problémom, musí mať primeraný počet výrobných zariadení určitý rezervný výkon/palivo a musí pracovať pod maximálnou kapacitou. Tieto zariadenia reagujú zvýšením svojho výstupného výkonu, aby nahradili stratený výkon a tým zastavili pokles frekvencie a vrátili systém do nového a správneho rovnovážneho prevádzkového bodu.
CIG vo svojej podstate neposkytujú zotrvačnú reakciu. Avšak teória aj prax preukázali, že CIG prispievajú k frekvenčnej reakcii [3], [4], [13], [14]. CIG môžu poskytovať primárnu frekvenčnú reakciu rýchlejšie, pretože limitujúcim faktorom v mnohých prípadoch (napr. solárne systémy a akumulácia energie) je reakčný čas výkonovej elektroniky a nie mechanických systémov (napr. kotlov a turbín). Keďže penetrácia CIG sa zvyšuje, je pravdepodobné, že frekvenčná reakcia energetických systémov bude mať tendenciu smerovať ku grafu zodpovedajúcemu menším systémom, ako je znázornené na obr. 5, ktorý kladie väčší dôraz na kvalitu a rýchlosť ovládacích prvkov spojených s primárnou frekvenčnou reakciou.
Vzhľadom na klesajúcu zotrvačnosť siete v dôsledku zníženia pomeru zastúpenia synchrónnych generátorov vo výrobe sa frekvenčné výkyvy stávajú rýchlejšími, a preto sa pravdepodobnosť nestability zvyšuje. To kladie väčší dôraz na potrebu navrhnúť vhodné, rýchlo pôsobiace regulátory na zastavenie poklesu frekvencie. Vysoký prienik CIG však nemusí viesť automaticky k výraznému zníženiu zotrvačnosti sústavy, a to v prípade, ak synchrónne generátory zostanú pripojené, ale nezaťažené. Frekvenčná reakcia sústav s CIG je komplexný jav, ktorý vyžaduje ďalší výskum.
V druhej časti seriálu sa budeme venovať opisu rezonančnej stability a stability riadenej meničom. Následne vysvetlíme pojem flexibility a predstavíme rôzne zdroje flexibility.
Poďakovanie
Táto práca vznikla s podporou Agentúry na podporu výskumu a vývoja SR na základe zmlúv APVV-19-0576 a APVV-21-0312 a Slovenskej akadémie vied na základe zmluvy VEGA 1/0757/21.
Literatúra
[1] Kaushik, E. – Prakash, problém V. – Mahela, O. P. – Khan, B. – El-Shahat Abdelaziz, A.: Comprehensive overview of power system flexibility during the scenario of high penetration of renewable energy in utility grid. In: MDPI Energies, 2022, vol. 15, iss. 2. [online].
[2] Kundur, P. et al.: Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. In: IEEE Transactions on Power Systems, 2004, vol. 19, no. 3, pp. 1387 – 1401. DOI: 10.1109/TPWRS.2004.825981.
[3] Hatziargyriou, N. et al.: Stability definitions and characterization of dynamic behavior in systems with high penetration of power electronic interfaced Technologies. In: IEEE Power and Energy Society, technical report PES-TR77, 2020. [online].
[4] Mattavelli, P. – Stankovic, A. M. – Verghese, G. C.: SSR analysis with dynamic phasor model of thyristor-controlled series capacitor. In: IEEE Transactions on Power Systems, 1999, vol. 14, no. 1, pp. 200 – 208.
[5] Contribution to Bulk System Control and Stability by Distributed Energy Resources Connected at Distribution Network. In: IEEE Power and Energy Society, Tech. Rep. PES-TR22, 2017. [online].
[6] Microgrid Stability, Definitions, Analysis, and Modeling. In: IEEE Power and Energy Society, Tech. Rep. PES-TR66, 2018. [online].
[7] Semlyen, A.: Analysis of disturbance propagation in power systems based on a homogenous dynamic model. In: IEEE Trans. Power App. Syst., 1974, vol. PAS-93, no. 2, pp. 676 – 684.
[8] Cresap, R. L. – Hauer, J. F.: Emergence of a new swing mode in the western power system. In: IEEE Trans. Power App. Syst., 1981, vol. 100, no. 4, pp. 2037 – 2045.
[9] Krištof, V. – Mešter, M: Loss of excitation of synchronous generator. In: J. Elect. Eng., 2017, vol. 68, no. 1, pp. 54 – 60.
[10] Machowski, J. – Bialek, J. W. – Bumby, J. R.: Power System Dynamics: Stability and Control. John Wiley & Sons Ltd 2008.
[11] Gibbard, M. J. – Pourbeik, P. – Vowles, D. J.: Small-signal stability, control and dynamic performance of power systems. The University of Adelaide Press 2015. Dostupné na: https://www.adelaide.edu.au/press/titles/small-signal.
[12] Dynamic Models for Turbine-Governors in Power System Studies. In: IEEE Power and Energy Society, Tech. Rep. PES -TR1, 2013. Dostupné na: https://resourcecenter.ieee-pes.org/technical-publications/technicalreports/PESTR1.html.
[13] Miller, N. – Lew, D. – Piwko, R.: Technology capabilities for fast frequency response, GE International Inc. Rep., 2017.
[14] Pourbeik, P. – Soni, S. – Gaikwad, A. – Chadliev, V.: Providing primary frequency response from photovoltaic power Plants. In: CIGRE Symposium, Dublin 2017.
Pokračovanie v ďalšom vydaní.
Ing. Marián Mešter, PhD.
Technická univerzita Košice
Katedra elektroenergetiky
Mäsiarska 74
042 10 Košice




![Obr. 1 Časová škála dynamických javov v elektrizačnej sústave [3]](/buxus/images/fotogaleria/atp_journal/kniznica_fotografii/fotogaleria_2024/_10_2024_stabilita_a_flexibilita_v_kontexte_bezpecnosti_elektrizacnej_sustavy_1_/dynamicke-javy-v-elektrizacnej-sustave.png)
![Obr. 2 Reklasifikácia stability elektrizačnej sústavy z dôvodu nasadenia OZE a DER s CIG [3], [4].](/buxus/images/fotogaleria/atp_journal/kniznica_fotografii/fotogaleria_2024/_10_2024_stabilita_a_flexibilita_v_kontexte_bezpecnosti_elektrizacnej_sustavy_1_/reklasifikacia-stability-elektrizacnej-sustavy.png)
![Obr. 3 Spôsoby modelovania stability elektrizačnej sústavy z dôvodu nasadenia OZE a DER s CIG [3], [4]](/buxus/images/fotogaleria/atp_journal/kniznica_fotografii/fotogaleria_2024/_10_2024_stabilita_a_flexibilita_v_kontexte_bezpecnosti_elektrizacnej_sustavy_1_/sposoby-modelovania-stabilizacnej-sustavy.png)
![Obr. 5 Príklady priebehu frekvenčnej reakcie pri veľkom systéme (červená), stredne veľkom systéme (modrá) a malom systéme (zelená) [3]](/buxus/images/fotogaleria/atp_journal/kniznica_fotografii/fotogaleria_2024/_10_2024_stabilita_a_flexibilita_v_kontexte_bezpecnosti_elektrizacnej_sustavy_1_/priklady-priebehu-frekvencnej-reakcie-elektrizacnej-sustavy.png)

